Diverse spatiotemporal dynamics in primate motor cortex local field potentials

Edit: this work has now been published as two papers. The first finds that mesoscopic beta-LFP oscillations may arise due to synchronization of rhythmic spiking in single neurons. The second  explores how changes in synchronization relate to the diverse patterns illustrated in the poster below.  

I'll present some of my ongoing thesis research at SfN as a poster this year. (This was originally titled "Identification of (~20 Hz) beta spatiotemporal dynamics in motor cortex LFPs".)

I've been looking into spatiotemporal waves in beta (~20 Hz) LFP oscillations during steady-state movement preparation. The wave dynamics seem to be more complex than previously reported [1, 2]. Patterns vary depending on the properties of the beta-LFP oscillations, perhaps reflecting phase synchronization dynamics between local modules, or a signature of external input? 

[PDF download]

Abstract:

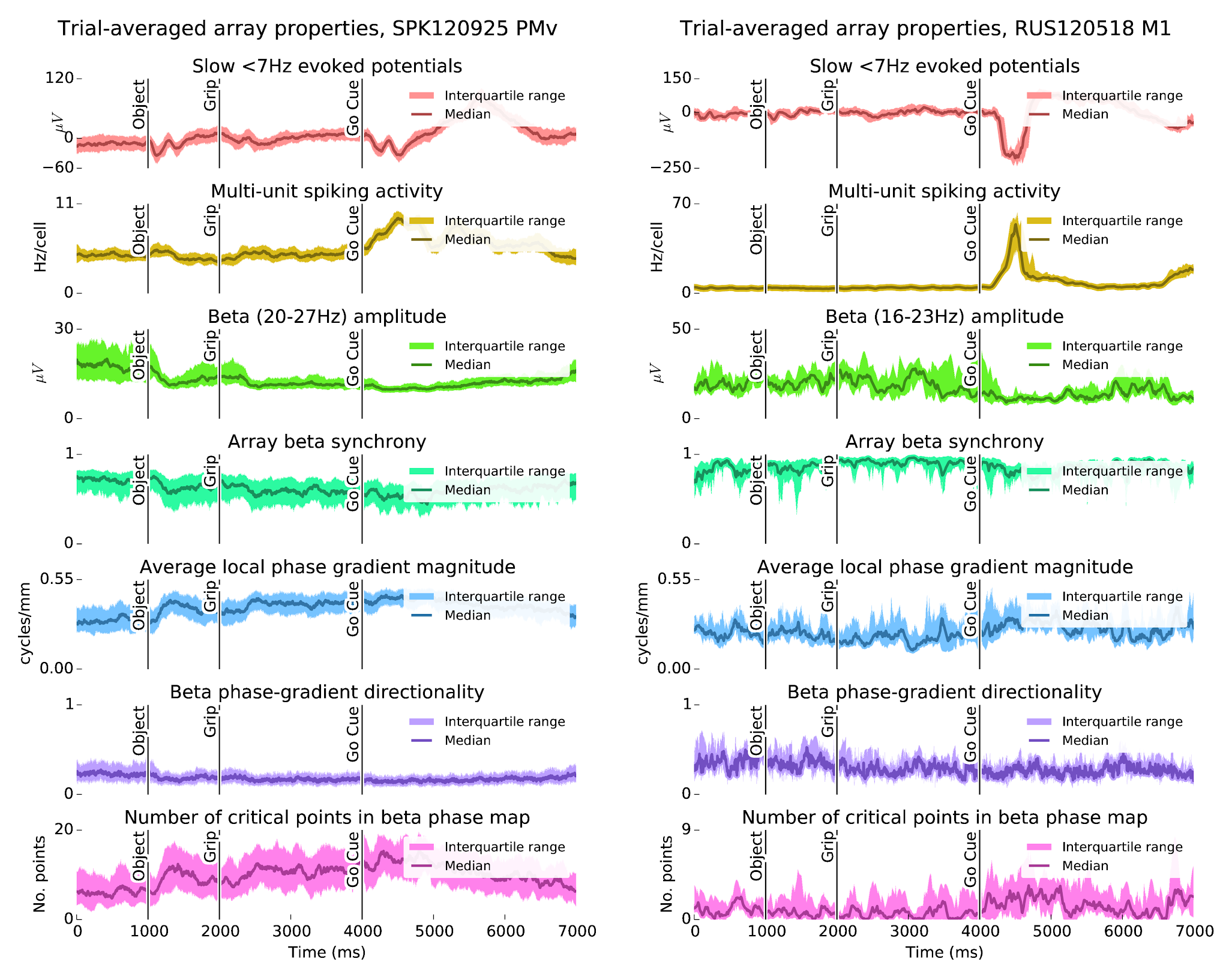
Modulation of beta (10-45Hz) oscillations is a prominent feature of primate motor cortex. Beta power is typically elevated during movement preparation, suppressed around movement onset, and enhanced during isometric force tasks. As shown by previous studies, beta oscillations can also appears as traveling waves in primate motor cortex. Understanding the mechanisms underlying the rapid modulation of beta LFP activity and the associated spatiotemporal patterns may shed light on the functional roles of these oscillations. It may also have important implications for movement disorders where regulation of motor cortex beta activity is abnormal (e.g. Parkinson's disease). Here, we examine motor cortex beta spatiotemporal LFP activity using multielectrode arrays (MEAs) in m. mulatta during a cued reaching and grasping task with instructed delay. Data from two monkeys are analyzed, each with a 96-MEA in ventral premotor cortex (PMv), and two 48-MEAs in the primary motor cortex (M1) and dorsal premotor cortex (PMd), respectively. Our main findings are threefold: (1) The transient nature of beta oscillation events together with variations in the beta band center frequency makes the identification of spatiotemporal structures challenging. In particular, different filtering and preprocessing steps can alter the apparent spatiotemporal dynamics. (2) Furthermore, attempts to summarize wave dynamics in terms of simple global structures, like plane waves, or rotating (radiating) waves around (from) a critical point, may fail to meaningfully describe the full range of beta spatiotemporal activity. (3) Despite these challenges, we find a variety of beta spatiotemporal patterns ranging from asynchronous states, i.e. states with no clear wave dynamics, to more locally synchronized states with complex wave dynamics, to globally coherent states. These globally coherent states may exhibit either traveling wave dynamics or homogeneous synchrony. We conjecture that the transitions among these different patterns may result from fast modulations of the effective lateral connectivity or from changes in spatiotemporal inputs to the cortical area.

This poster can be cited as

Rule, M. E., Vargas-Irwin, C., Donoghue, J., Truccolo, W. (2015) Identification of (~20 Hz) beta spatiotemporal dynamics in motor cortex LFPs. [Poster] Society for Neuroscience 2015, Oct 19th, Chicago, Il, USA. 

Update: This work can now be found in the following papers

Rule, M.E., Vargas-Irwin, C.E., Donoghue, J.P. and Truccolo, W., 2017. Dissociation between sustained single-neuron spiking and transient β-LFP oscillations in primate motor cortex. Journal of neurophysiology, 117(4), pp.1524-1543. 

Rule, M.E., Vargas-Irwin, C., Donoghue, J.P. and Truccolo, W., 2018. Phase reorganization leads to transient β-LFP spatial wave patterns in motor cortex during steady-state movement preparation. Journal of neurophysiology, 119(6), pp.2212-2228.

Contribution of LFP dynamics to single-neuron spiking variability in motor cortex during movement execution

My first Ph.D. publication is out! Contribution of LFP dynamics to single-neuron spiking variability in motor cortex during movement execution explores how the activity of individual neurons in motor cortex is related to population activity, as measured by electrical Local Field Potentials (LFPs). 

[get PDF] 

How do the actions of individual cells combine to create the emergent dynamics that underlie perception, thought, and action? To answer this question, we should study populations of single neurons, and ask how their activity is related to measures of collective population dynamics. This study was a collaboration between the Truccolo and Donoghue labs, and looked at neural population recordings from primate motor cortex during movement.

We found that the activity of single cells was tightly coupled to population activity as measured by LFPs, and that both of these signals were closely realated to movement. This suggest that, during movement execution, collective dynamics reflected in motor cortex LFPs mostly reflect the sensorimotor processes directly controlling movement output. It also suggests that primary motor cortex isn't engaged in other activities like cognition or future planning, while executing movements.

Importantly, we considered both past and future movement in this analysis, and found that single neurons and LFPs both contain information about recent and upcoming movements. This is consistent with the view that motor cortex acts as a dynamical pattern generator.

Many thanks to Carlos Vargas-Irwin, John P. Donoghue, and Wilson Truccolo. The article is open access, and you can also grab the PDF from Github. The paper can be cited as:

Rule, M.E., Vargas-Irwin, C., Donoghue, J.P. and Truccolo, W., 2015. Contribution of LFP dynamics to single-neuron spiking variability in motor cortex during movement execution. Frontiers in systems neuroscience, 9, p.89. 

 

Figure 4. Breakdown of LFP predictive power by frequency band and LFP feature. Box-plots over the population of isolated units (all sessions combined) showing the predictive power of models based on phase, amplitude, or analytic signal features in isolation from each of eight LFP bands. To better assess the individual predictive power of each LFP feature, models were fitted for each feature separately. Certain features, such as the instantaneous phase and analytic signal for the 0.3–2 Hz band, as well as the analytic signal amplitude modulation above 100 Hz, consistently predict spiking across all animals and areas.

Directional statistics for spatiotemporal wave analysis

I've been searching for a good distribution that can be used to summarize how the distribution of phases and amplitudes evolves during transient synchronization events of beta (~20 Hz) local field potentials (LFP) in motor cortex. So far, it seems difficult to find a single distribution family that works in all cases. 

Spatiotemporal wave activity in beta oscillations in motor cortex can be described in terms of the beta-band analytic LFP signal, which has both a magnitude and a phase, and who's real part is equal to the time-domain value of the beta-filtered signal. 

\begin{equation}z_k(t) = \beta_k (t) + i\cdot  \operatorname{Hilbert}(\beta_k)(t) = r_k(t) e^{i \theta_k(t)},\\\textrm{ where $k$ indexes over channels}\end{equation}

Circular statistics can be used to summarize the distribution of analytic signal phase, in order to detect synchrony and wave events.

[read more in the PDF

Figure 2: Neither the complex Gaussian nor log-polar statistics perfectly describe the distributions of analytic signal. In these plots, the black ellipse represents a complex Gaussian model of the data, with the ellipse boundary at one standard deviation, and the ellipse axes representing the eigenvectors of the covariance matrix $\Sigma$. The cyan contours represent a log-polar model of the data, which uses the mean and standard deviation of the log-amplitude, as well as the circular mean and standard deviation of the phases, to model the data in log-polar space. (a) When phase is concentrated, and not correlated with amplitude, both the log-polar statistics and the complex Gaussian distribution describe the data well. (b) When phase and amplitude are correlated, the log-polar model cannot capture the phase-amplitude dependence. (c) During traveling wave events, signal amplitude is high, and there is dispersion in phase. In these cases, the log-polar statistics are more appropriate than the complex Gaussian. (d) Traveling wave events appear to often evolve from states that show a mixture of synchrony and standing wave dynamics. The log-polar statistics break down when the phase distribution is bimodal, but the complex Gaussian can describe these states well. (e) At low signal amplitudes, the system is often asynchronous, and the phase and amplitude of the log-polar model are poorly defined. (f) Although rare or absent in our data, a hypothetical distribution with uniform phase and concentrated amplitude could occur, say, during traveling wave events with short wavelength. In this case, the complex Gaussian model is especially bad.

Three unbiased estimators of spike-field coherence

[get notes as PDF]

In these notes we show a simplified expression for the Pairwise Phase Consistency (PPC) measure of Vinck et al. (2010). We illustrate it's relation to a bias-corrected spike-field coherence measure from Grasse et al. (2010), and discuss an third notion of spike-field coherence that is intermediate between the two. 

Here, we use the term "event-triggered" rather than "spike-triggered", because we want to apply these measures to neural events other than spikes (e.g. beta-frequency transients in motor cortex).

Pairwise Phase Consistency

Vinck et al. (2010) define Pairwise Phase Consistency (PPC) as the expected dot product between all pairs of (spike-triggered) phase measurements. 

\[\hat\Upsilon = \frac 2 {N(N-1)} \sum_{j=1..N-1} \sum_{k=j+1..N} \cos(\theta_j - \theta_k)\]

There is an alternative way to express PPC that is faster to calculate, and also reveals a relationship between PPC and similar alternatives. 

Motor cortex LFP spatiotemporal dynamics in a cued grasp with instructed delay task

Update: Portions of these notes have now been published in the Journal of Neurophysiology as  "Dissociation between sustained single-neuron spiking and transient β-LFP oscillations in primate motor cortex" and "Phase reorganization leads to transient β-LFP spatial wave patterns in motor cortex during steady-state movement preparation".

[get notes as PDF]

Task-locked modulations in neural activity

The Cued Grasp with Instructed Delay (CGID) task reliably elicits task-locked activity in all three motor areas (M1, PMd, PMv).

• Consistent with prior literature, the movement period of the CGID task is marked by slow motor evoked potentials (Fig. 2), increased single-unit firing rates (Fig. 3), and beta suppression (Fig. 4).
• Beta oscillations are enhanced during the first four seconds of the task, although there are some differences between subjects.
• The average level of beta-LFP synchrony is correlated with beta-LFP power, and varies across phases of the task.
• We find no evidence of task-locked phase resetting of beta LFP oscillations
• The spatiotemporal structure of beta-LFP waves is correlated with amplitude and synchrony, with lower amplitudes reflecting more complex wave structures, and higher amplitudes as more synchronous.

Figure 1: The CGID task reliably elicits evoked potentials, which correlate with beta suppression. In subject S, beta power is strongest in the first second before object presentation. In subject R, beta oscillations are more variable, with somewhat stronger power between the grip and go cues. In both animals, high beta power appears to correspond to periods of higher beta synchrony, and larger phase gradient directionality, a measure of how much LFP activity resembles a plane wave. Conversely, increases in the average magnitude of the Hilbert phase gradient, which summarizes how quickly beta phase changes over the array, and in the number of critical points in the Hilbert phase gradient, which summarizes the complexity of the beta spatiotemporal wave patterns, correspond to periods of beta suppression.