Neural field models for latent state inference

The final paper from my Edinburgh postdoc in the Sanguinetti and Hennig labs (perhaps, we shall see). 

[get PDF]

We combined neural field modelling with point-process latent state inference. Neural field models capture collective population activity like oscillations and spatiotemporal waves. They make the simplifying assumption that neural activity can be summarized by the average firing rate in a region.

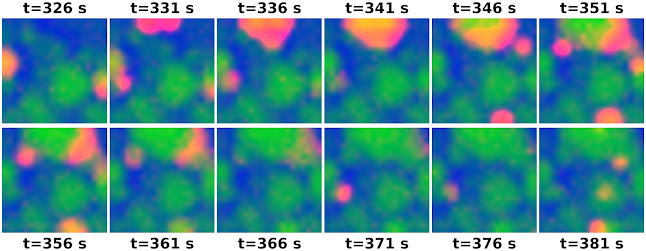
High-density electrode array recordings can now record developmental retinal waves in detail. We derived a neural field model for these waves from the microscopic model proposed by Hennig et al.. This model posits that retinal waves are supported by an quiescent, active, and refractory states. 

Fig 3. Spatial 3-state neural-field model exhibits self-organized multi-scale wave phenomena. Simulated example states at selected time-points on a [0,1]² unit interval using a 20×20 grid with effective population density of $\rho{=}50$ cells per unit area, and rate parameters $\sigma{=}0.075$, $\rho_a {=} 0.4$, $\rho_r {=} 3.2 \times 10^{−3}$, $\rho_e {=} 0.028$, and $\rho_q {=} 0.25$ (Methods: Sampling from the model). As, for instance, in neonatal retinal waves, spontaneous excitation of quiescent cells (blue) lead to propagating waves of activity (red), which establish localized patches in which cells are refractory (green) to subsequent wave propagation. Over time, this leads to diverse patterns of waves at a range of spatial scales. 

Neural field models usually just describe mean activity, but we used a second-order neural field model that also models noise and correlations. The mean and correlations describe the latent neural state as a Gaussian process. We then modeled the observed spiking as a Poisson point-process driven by this latent activity. Our method of inferring latent Gaussian state builds on the work of Andrew Zammit Mangion, Botond Cseke, and David Schnoerr.

Overall, it worked, and we got some beautiful wave videos out of it. (We also applied this method to infer parameters, which mostly worked, but not quite well enough to put into the manuscript.)

Mouse retina, P10, 10x real-time

Many thanks to Gerrit Hilgen, Evelyne Sernagor, David Schnoerr, Dimitris Milios, Botond Cseke, Guido Sanguinetti, and Matthias Hennig. 

The code is on Github, and the paper can be cited as

Rule, M.E., Schnoerr, D., Hennig, M.H. and Sanguinetti, G., 2019. Neural field models for latent state inference: Application to large-scale neuronal recordings. PLoS computational biology, 15(11), p.e1007442. 

Epilogue

In retrospect, there are a couple more things I would have liked to try

• It could be promising to try the Unscented Kalman Filter (UKF). The Gaussian neural field equations we used result (essentially) in an Extended Kalman Filter (EKF), once space and time are discretized. EKFs have stability issues if the latent-state density is non-Gaussian, or if local derivatives are a poor estimate of the average derivatives across the state distribution. The UKF, as I understand it, might side-step these issues.
• René et al. had impressive success in inferring a model from data using a similar (but more sophisticated) approach. Key advantages: they had more complete observations, and weren't trying to infer high-dimensional spatially-extended neural field states. 
• We inferred the whole retina state simultaneously. We were limited to spatial grids with <600 elements. This wasn't just for speed: finer spatial scales are increasingly redundant, making the covariance ill-conditioned. Simulating regional patches separately, and then stitching them together to cover the field, might have been better.

Unpublished figure: Parameter inference using filtered model log-likelihood. Shown here are the results of inferring the excitation rate ($QA\to AA$; $\rho_e$) and recovery/refractoriness rate ($A\to R$; $\rho_a$). Likelihood was computed via Bayesian filtering using the inferred latent neural field states. Eight retinal wave datasets were analyzed, ranging from age P4 to P11. Both excitability, and the rate at which cells leave the active state, increases with age. This is consistent with an increase in the speed, and frequency of waves with age. All other parameters were fixed manually in an ad-hoc way (likelihood inference for slow parameters failed, see Results: Open challenges in model identification)