Neural field models for latent state inference

The final paper from my Edinburgh postdoc in the Sanguinetti and Hennig labs (perhaps, we shall see). 

[get PDF]

We combined neural field modelling with point-process latent state inference. Neural field models capture collective population activity like oscillations and spatiotemporal waves. They make the simplifying assumption that neural activity can be summarized by the average firing rate in a region.

High-density electrode array recordings can now record developmental retinal waves in detail. We derived a neural field model for these waves from the microscopic model proposed by Hennig et al.. This model posits that retinal waves are supported by an quiescent, active, and refractory states. 

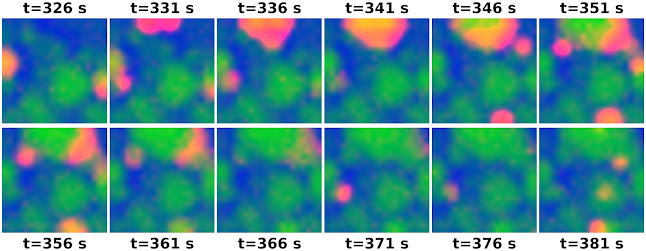Fig 3. Spatial 3-state neural-field model exhibits self-organized multi-scale wave phenomena. Simulated example states at selected time-points on a [0,1]² unit interval using a 20×20 grid with effective population density of $\rho =50$ cells per unit area, and rate parameters $\sigma =0.075$, ${\rho }_a=0.4$, ${\rho }_r=3.2\times {10}^{-3}$, ${\rho }_e=0.028$, and ${\rho }_q=0.25$ (Methods: Sampling from the model). As, for instance, in neonatal retinal waves, spontaneous excitation of quiescent cells (blue) lead to propagating waves of activity (red), which establish localized patches in which cells are refractory (green) to subsequent wave propagation. Over time, this leads to diverse patterns of waves at a range of spatial scales. 

Moment equations for an autoregressive point process with an absolute refractory period

These notes extend the autoregressive point-process moment closures derived in Rule and Sanguinetti (2018) to models that include an absolute refractory period via a gating term that sets the rate to zero after a spike.

[get notes as PDF]